Kapitel 11
Kapitel 11 Kapitel 11
Kapitel 11Many design decisions can be expressed in the form of: IF Shape grammars are concerned with the development and application of rules that operate on shapes to generate compositions. A convenient notation for the expression of rules is to view the left hand side (LHS) of rule expressing as an IF condition, and the right hand side (RHS) as a THEN action.
Following three examples illustrate basic concepts underlying shape grammars.
Example 1:
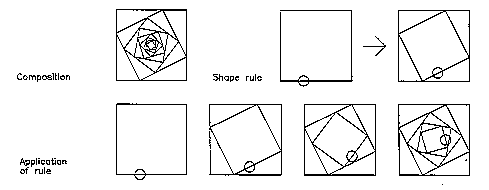
A number of graphic compositions as well as natural objects follow very precise geometric constructions. For example, the composition shown above is developed by rotating and placing a smaller square inside another one, where the amount of rotation and reduction in size can be expressed using a single rule. The second row in the above illustration shows successive applications of this rule to an initial shape.
Example 2:
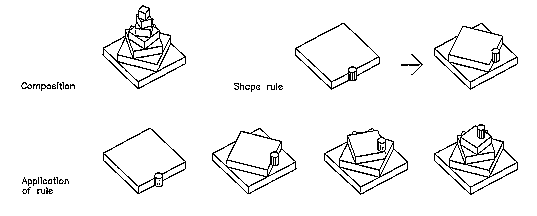
Example 2 is similar to the previous one except that the composition is extended into the third dimension. An object is placed on top of another one by rotating and scaling its size by a fixed amount as expressed in the rule of composition. Again, we have one rule and one initial shape to which the rule is applied a number of times.
In these two examples, a rule is made up of a left hand side (LHS) which specifies the context and the right hand side (RHS) which specifies the action. In other words, if a shape such as specified on the LHS is found in the composition, we replace that shape with the one given on the RHS. Since our grammar deals with shapes that are geometric in nature, we make use of labels (shown as small circles in the examples) to unambiguously define the rule applications. What do the labels in the above two examples signify?
In previous examples, a shape on the LHS is replaced by another one on the RHS as specified by the rules. And in both cases, shapes on the RHS preserve spatial relations between lines: their relative lengths and angles between them. It is also possible to define rules that change these spatial relations as shown in the next example.
Example 3:
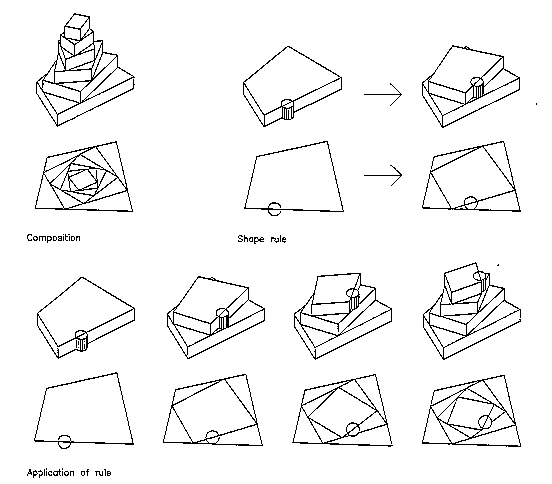
In this example, the rule can be stated as: given an arbitrary oblong with a label on an edge, divide the remaining three edges in proportion to the labeled edge, and inscribe a new labeled oblong using these points and the label. The bottom row shows the rule application on an initial shape. This example shows the emerging composition in both plan and 3D views.
Shape grammars are defined in terms of: a set of shapes, a set of labels, a set of shape rules, and an initial shape. Each shape rule is of the form A -> B where A and B are made up of elements in the sets of shapes and labels.
Where the spatial relations between elements of shapes - their relative lengths and angles between them, are maintained in shape rules, such grammars are known as standard shape grammars. If these relations are allowed to change, such grammars are known as parameterized shape grammars.
Consistent application of rules contained in a grammar will produce all possible compositions that are syntactically correct, thereby defining a language of expression.
To make you familiar with how to encode shape grammar rules in AutoLisp, source files for all three examples given above are provided. Program files are: 11_shape1.lsp, 11_shape2.lsp, 11_shape3.lsp. A menu file is also provided: 11_shape.mnu. All these files are in the directory /homes2/prog/ausgabe. You should copy these files into your directory and run these programs. Study the program code to understand how to implement shape rules in AutoLisp.
In architectural design, shape grammars can be used to explore various design languages as well as to discover rules underlying a set of related designs.
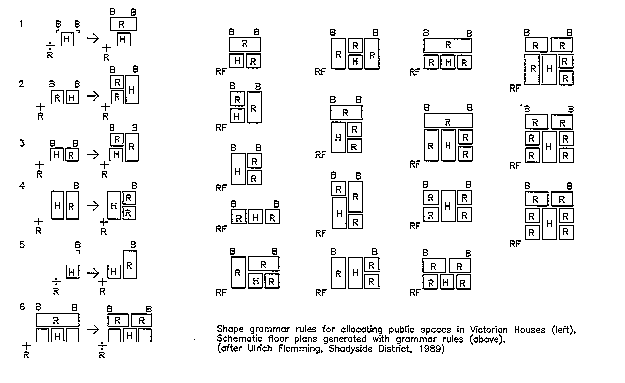
Following example by Flemming el al. uses existing residential designs to discover a set of rules that capture characteristics of an architecturally distinct neighborhood in Pittsburgh, USA. (Source: The Shadyside Project, Ulrich Flemming et al.)
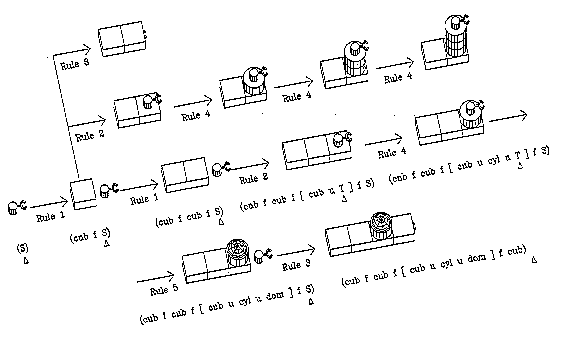
In this exercise you will write an interpreter for grammars that can generate compositions of geometric shapes. The grammars we will be using do not generate geometry directly, instead, they generate lists of symbols. Such lists are then used to instruct an imaginary robot, which understands a set of predefined instructions (symbols), to build a geometric composition out of a set of primitive building blocks. The following is a list of symbols that the robot understands:
The definition of a grammar includes two parts: an axiom and a set of rules. An axiom consists of a list of symbols serving as the starting "seeds" of the generation process. The rules define how those "seeds" can be further developed. The result of recursive application of these rules to the axiom is a list of instructions to the robot. The process may not be deterministic, that means sometimes there is more than one way of applying rules. We solve this problem by asking the user to make a decision when an ambiguity occurs. A grammar can be represented as a list. The first element of the list is the axiom, which is a list of symbols. The second element is a list of rules. Each rule consists of a condition part and an action part. In this exercise, the condition of each rule consists of exactly one symbol which is not a primitive instruction to the robot. The actions this symbol implies are described in the action part of the rule. The following is an example of a grammar :
This grammar describes an infinite set of compositions. It can generate sequences of cubes with one or more cylindrical towers.
One possible derivation of the given grammar.
/homes2/prog/ausgabe/11_robot.bi4 is a program that simulates the robot. Read the file 11_uebung.readme to understand how to use the various functions. Your task is to write a function called "compose", which accepts the definition of any well-formed grammar as input. The function will expand the axiom by substituting the actions of the applicable rules for the conditions, and issues instructions to the robot accordingly. When more than one rule is applicable, prompt the user to select one of them. Use the sample grammar to test your compose program and save it as 11_name.lsp. Once the program is completed, define a new grammar that generates interesting compositions. Add your grammar to the compose program as a list assigned to a variable. Try to define a grammar that generates only the compositions you want, for example, symmetrical U shapes with towers in the corners. Create a slide file named 11_name.sld to show some compositions generated by your grammar using your compose function. Send a copy of your program and slide files to /homes2/prog/abgabe.
The purpose of this exercise is to experience what grammars can do and what they can not. Ways of extending grammars as well as restricting them are important foundations of computer science. Depth first search and breadth first search are important techniques in the paradigm of artificial intelligence. The basic distinction between the two approaches should be evident in this exercise.
Prog
Content
Vorwort
..1..
..2..
..3..
..4..
..5..
..6..
..7..
..8..
..9..
..10..
..11..
..12..
..13..
Appendix
11.1 Geometric Compositions
11.2 Shape Grammar
11.3 Architectural Design
11.4 Uebung 11